人机协同下的宽容式反应型机器人任务规划
摘要
本文提出了一种新颖的人机逻辑交互框架,该框架能让机器人在与执行独立且未知任务的人类高效协作的同时,可靠地完成(无限时间范围的)时序逻辑任务。该框架具备两大核心能力:一是最大适应度,机器人可在线调整策略,在任何可能的情况下利用人类行为实现协作;二是最小可调反馈,机器人仅在确保任务推进必需时,才会在线请求人类配合。这种平衡设计能最大程度减少人机干扰、保障人类自主性,即便在人类目标与机器人目标冲突的情况下,也能确保机器人持续完成任务。我们在真实世界场景中,通过 Franka Emika Panda 机械臂完成积木操作任务,并在 OvercookedAI 基准测试中验证了该方法 —— 结果表明,该方法能产生现有方法无法实现的丰富、新兴协作行为,同时还能提供强有力的形式化保障。
1 引言
高效的人机交互(HRI)要求机器人与追求自身目标的人类协同工作,而人类往往不会明确透露其目标。这类场景在智能制造、物流、医疗辅助机器人、家庭服务机器人等领域的应用日益广泛。在这些场景中,机器人不仅要规划动作以完成自身任务,还需在线适应人类行为 —— 人类行为可能是协作性的、中立的,甚至可能阻碍机器人任务。同时,若机器人不仅能对人类行为做出反应,还能尊重甚至利用人类行为,而非一味地推翻或限制人类行为,人机交互会更高效,人类体验也会更愉悦。

本文针对人机时序交互(HRωI) 场景下的这一挑战展开研究:机器人需执行以线性时序逻辑(LTL)表达的高层时序任务,而人类则同时执行未知的、潜在的策略性任务。以图 1 所示的简化操作任务为例,Franka Emika Panda 机械臂与人类轮流在 3×3 区域内放置积木。机器人的任务是确保最终大多数格子被积木占据,且没有相邻格子被填充;而人类的隐藏目标是形成一条对角线。若逻辑任务的范围受限(如本示例),人机所有可能的策略性交互都可编码为双人博弈图,如图 2 所示。该图中的特定状态分别满足机器人(或人类)的目标,是机器人(或人类)希望反复到达的状态。但由于机器人和人类都能移动积木,双方都可能阻碍对方达成目标。值得注意的是,即便双方目标相同(如都想形成对角线),也可能出现阻碍情况。例如,人类坚持形成从西南到东北的对角线,而机器人坚持形成从东南到西北的对角线,最终会导致 “活锁”(双方陷入循环、无法推进任务)。若人机目标不同甚至完全冲突,这一问题会更加严重。
为解决这一问题,本文提出了一种新颖的 HRωI 框架:该框架能让机器人持续完成逻辑任务,同时在任何可能的情况下保障人类自主性,仅在必要时请求人类协作。
1.1 相关工作
由于可靠的人机交互(HRI)对可信自主性至关重要,该研究领域已积累了大量成果 ¹。因此,本文仅聚焦于以 “人机博弈” 为核心的 HRωI 场景。这一研究方向源于两篇开创性论文 [1][2],其核心观点是:线性时序逻辑(LTL)是一种强大的规范语言,可用于描述策略性目标,如自动驾驶的交通规则 [3]、机器人导航 [4] 等。
人机时序交互(HRωI)的一种常见建模方式是 “机器人 – 环境” 双人博弈。目前已有大量关于图博弈的研究 [5]-[12],可用于计算机器人的反应型策略,以完成各类复杂任务。但遗憾的是,多数解决方案要么过度限制机器人,要么过度限制人类:
- 第一种情况:为机器人计算能对抗所有人类策略、确保自身目标达成的策略。但这种方案限制性过强,在上述积木操作等场景中,往往无法生成有效的机器人策略。
- 第二种情况:假设人机完全协作,为双方计算共同策略。但这会将人类束缚在僵化、高度受限的行为模式中 —— 虽能保证任务可靠性,却牺牲了人类的自主性。
部分研究提出了 “中间方案”,以提升人类自主性:若仅关注逻辑安全性(即避免人机间产生不良策略性交互),可采用 “反应型屏蔽机制”[13]-[16],仅在可能出现不良交互时干预人类行为。但如果存在逻辑活性目标(即要求 “好事” 最终发生,如上述示例中 “形成对角线”),安全性屏蔽机制无法保证规范的满足(如前文提及的 “人机均想形成对角线却陷入活锁” 的情况)。
为缓解这些问题,许多研究明确对人类行为进行建模 —— 要么通过轨迹预测 [17],要么将其表示为马尔可夫决策过程 [18]—— 并将这些模型融入综合框架。此外,人机时序交互(HRωI)也可直接建模为随机双人博弈 [19]。这种方式虽能通过随机性体现人类策略的局部可行性,但无法满足人类策略自主性的需求。
为进一步提升人类自主性,可采用基于 “可接受性” 的方法 [20][21]:这类方法能让机器人在确保任务完成的同时,采用对多种人类行为都具备鲁棒性的行为。与之不同,Schuppe 等人 [22] 聚焦于 “交互式建议”:机器人通过 “假设 – 保证” 式指导向人类提供建议,以最少的人类协作支持共同目标的达成。但这些方法存在局限:机器人需绑定预计算的固定策略,且要么对人类行为有严格假设,要么依赖静态、预定义的建议形式。
另一类相关研究仅为机器人设定(非反应型)逻辑规划目标,并通过 “控制屏障函数(CBF)” 在机器人工作空间中保障人类安全 —— 控制屏障函数可作为底层连续机器人动力学的安全过滤器 [23]。近年来,该方法被整合到协作式 HRωI 框架中 [24]-[26]:在这些框架中,人机双方的(反应型)逻辑目标均为已知,因此可通过离线集中式博弈求解。但人机在线适应仅在物理底层通过控制屏障函数实现,不存在策略层面的自主性。类似地,近期针对人机交互的动态博弈研究 [27][28] 也聚焦于即时物理交互,而非人机长期的策略性适应与交互。
与上述方法不同,本文提出的 HRωI 方法以 “自主性” 为核心,聚焦高层策略性交互。此前的相关研究 [20]-[22][29][30] 虽也关注这一方向,但最终会生成预计算的协作或反馈形式,且仅考虑有限时间范围的目标;而本文框架通过 “在线适应” 与 “可调反馈” 的协同,为有限和无限时间范围的 LTL 任务生成复杂的新兴协作行为。从形式化角度而言,该新颖框架的实现依赖于 “ω- 正则博弈” 的宽容式策略模板 [31](由 LTL 目标推导而来),这种模板可简洁地表示无限多种策略。策略模板已在多个领域得到应用 [32]-[39],但据我们所知,本文首次将其应用于 HRωI 场景。具体而言,我们借鉴了 [33] 中的最新成果 —— 该成果可捕捉所有能在 “最小协作” 下保证 φ(任务目标)满足的人机策略,为本文提出的 “具备强形式化保障的在线适应” 提供了理论基础。
1.2 研究贡献
本文的核心贡献是一个通用的 HRωI 框架,该框架适用于所有类型的 LTL 任务,且不假设人类会进行特定的策略性协作。从概念上讲,该框架让机器人不再将人机交互仅视为 “需限制的不确定性来源”,而是更多地将其视为 “可利用的资源”。在执行高层 LTL 任务 φ 时,机器人策略具备两大特点:
- 运行时适应人类行为:例如,若人类希望形成 “西南 – 东北” 方向的对角线,机器人会顺应这一行为,而非坚持形成另一方向的对角线,以在任何可能的情况下最大化协作;
- 仅在必要时提供策略性反馈:当仅靠机器人自身适应无法确保 φ 的推进时(例如,人类持续移除中间积木,阻碍对角线形成),机器人才会请求人类停止该行为。
这种设计能最大程度减少人机干扰、提升协作效率、保障人类自主性,同时若人类最终听从反馈,还能确保机器人任务的最终完成。
我们通过仿真和机器人硬件实验验证了该方法:除图 1 所示的机器人积木操作场景外,还在 Overcooked-AI 仿真环境 [40](多智能体协作规划的常用基准测试平台)中对框架进行了评估。在该环境中,人机需反复执行烹饪任务,目标是持续制作汤品。双方各有独立的 LTL 任务(编码为食谱规范),且任务彼此保密。人类行为通过概率策略模拟。
在这一应用场景中,“ω- 正则规范” 相比常用的 “可达性任务” 的优势愈发明显:由于双方都需尽可能制作符合自身规范的汤品,即便规范冲突,也可通过 “轮流制作符合各自规范的汤品” 实现协作。实验表明,通过本文框架的在线适应与反馈机制,这种直观的协作行为能自主涌现。据我们所知,该框架产生的 HRωI 新兴行为的复杂性远超现有所有方法,同时还能提供形式化保障。
2 问题设定
本文聚焦于 “轮流行动” 的人机交互场景:机器人与人类在共享环境中交替行动。给定机器人的高层时序任务,本文的目标是开发一个框架,让机器人能基于观察到的人类行为在线调整策略,并以规范、可调的方式提供反馈 —— 即便人类执行独立目标且其策略可能阻碍机器人任务推进,也能确保机器人可靠完成任务。
2.1 反应型规划域
我们将人机交互建模为反应型规划域\(D=<S, s_0, A, AP, L>\),各元素定义如下:
- \(S = S_r \cup S_h\):状态集合,分为机器人状态\(S_r\)和人类状态\(S_h\);
- \(s_0 \in S\):初始状态;
- \(A = A_r \cup A_h\):动作集合(建模为有向边),分为机器人动作\(A_r \subseteq S_r \times S_h\)和人类动作\(A_h \subseteq S_h \times S_r\);
- AP:与任务相关的命题集合,每个命题在特定状态下要么为 “真”,要么为 “假”;
- \(L: S \to 2^{AP}\):标签函数,为每个状态分配一组 “为真的命题”。
规划域可通过 “规划域定义语言(PDDL)”[41] 描述 —— 这是 AI 规划领域的标准语言。在 PDDL 描述中,“状态” 捕捉相关对象及其位置,“动作” 通过 “前置条件” 和 “效果” 定义。
规划域的 “运行轨迹”\(\rho = s_0 s_1 s_2 \dots\)是无限状态序列,满足\(s_0\)为初始状态,且对所有\(i \geq 0\),存在动作使系统从\(s_i\)转移到\(s_{i+1}\)(即\((s_i, s_{i+1}) \in A\))。运行轨迹\(\rho\)会生成 “迹”\(L(\rho) = L(s_0) L(s_1) L(s_2) \dots\)—— 这是一个基于\(2^{AP}\)的无限字符串,对应轨迹中各状态的标签序列。本文假设人机轮流行动:若\(s_i \in S_r\)(当前为机器人状态),则\(s_{i+1} \in S_h\)(下一状态为人类状态),反之亦然。
机器人策略\(\pi_r: S^* S_r \to A_r\)是一个函数:将 “以机器人状态结尾的交互历史(状态序列)” 映射为机器人应执行的动作。若对所有\(i \geq 0\),当\(s_i \in S_r\)时,\(s_{i+1} = \pi_r(s_0 s_1 \dots s_i)\),则运行轨迹\(\rho = s_0 s_1 s_2 \dots\)称为 “\(\pi_r\)- 轨迹”。人类策略\(\pi_h\)和 “\(\pi_h\)- 轨迹” 的定义与此类似。
示例 1:图 2 展示了 “轮流人机交互” 反应型规划域的部分视图。每个圆形节点(如 r0、r1…)对应\(S_r\)中的机器人状态,每个矩形节点(如 h0、h1…)对应\(S_h\)中的人类状态。节点内部的 3×3 网格代表环境:红色方块为人类放置的物体,蓝色圆形为机器人放置的物体。边代表动作集合A中的动作,根据轮流交互规则在人机动作间交替。例如,从状态 r2 到 h2 的边代表 “机器人移除(1,1)格子(即第 1 行第 1 列)中蓝色圆形物体” 的动作。图 1 展示了 Franka 机械臂在真实场景中执行该动作的画面。
标签函数L可用于捕捉AP中与任务相关的命题。例如,设\(AP = \{adj, diag, major\}\),各命题含义如下:
- adj:无两个物体相邻(水平或垂直方向);
- diag:一条对角线被完全占据;
- major:9 个格子中至少 4 个被占据(多数占据)。
在这种定义下,仅状态 r0、t1、t2 满足\(adj = 真\);状态 r5、t2 满足\(diag = 真\);除 h0 和 r0 外,所有状态均满足\(major = 真\)。从初始状态 h0 出发,一个可能的运行轨迹为\(\rho = h0 (r1 h1 r2 h2)^\omega\)(“\(\omega\)” 表示循环),其生成的迹为\(L(\rho) = \{major\}^\omega\)(即所有状态均满足 “多数占据”)。
2.2 作为 LTL 公式的时序任务
为表达人机任务,我们采用 “线性时序逻辑(LTL)”—— 这是一种在命题逻辑基础上扩展了时序算子的规范语言 [42]。给定原子命题集合AP,LTL 公式通过以下规则递归定义:
\(\varphi ::= \top | p | \neg \varphi | \varphi_1 \land \varphi_2 | \bigcirc \varphi | \varphi_1 \mathcal{U} \varphi_2\)
其中:
- \(p \in AP\):原子命题;
- \(\neg\)、\(\land\):布尔算子(否定、合取);
- \(\bigcirc\)、\(\mathcal{U}\):时序算子(“下一个”、“直到”)。
其他标准算子(如析取\(\lor\)、蕴含\(\rightarrow\)、“最终”\(\diamond\)、“全局”\(\square\))可由上述算子推导得出。LTL 公式的语义基于\((2^{AP})^\omega\)中的无限原子命题集合序列,详细定义可参考相关标准文献 [43, 第 5.1.2 章]。若运行轨迹\(\rho\)生成的迹满足 LTL 公式\(\varphi\),则称\(\rho\)满足\(\varphi\),记为\(\rho \vDash \varphi\)。
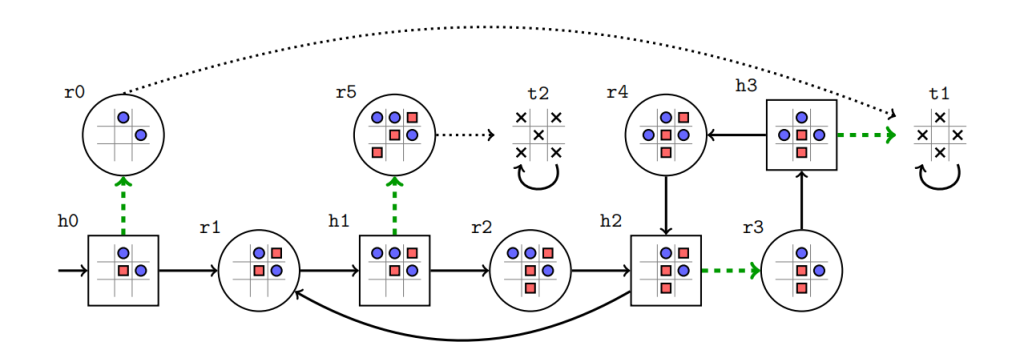
示例 2:再次考虑示例 1 中的反应型规划域,原子命题集合\(AP = \{adj, diag, major\}\)。假设机器人任务是 “反复到达‘无物体相邻且多数格子被占据’的状态”,该任务可表示为 LTL 公式\(\varphi_r = \square \diamond (adj \land major)\)(“\(\square\)” 表示 “始终”,“\(\diamond\)” 表示 “最终”)。人类任务可能是 “反复到达‘对角线被完全占据’的状态”,可表示为\(\varphi_h = \square \diamond diag\)。若运行轨迹反复经过状态 t1,则该轨迹同时满足\(\varphi_r\)和\(\varphi_h\);若轨迹最终仅在状态 t2 循环,则仅满足\(\varphi_r\)。
2.3 问题描述
本文研究的人机交互场景中,双方各有独立任务且彼此未知。在这类场景中,即便并非故意,一方的策略也可能阻碍另一方的任务推进。本文的目标是开发一个框架,让机器人能:
- 基于局部观察调整策略;
- 在必要时向人类提供反馈;
- 最终持续完成自身任务。
问题 1:给定 “人机交互反应型规划域D” 及 “机器人的 LTL 任务\(\varphi\)”,且人类执行未知的潜在任务,需开发一个框架满足以下要求:
- 捕捉所有能让机器人完成\(\varphi\)的人类协作行为;
- 基于交互过程中观察到的人类策略行为,调整机器人策略;
- 整合可调反馈机制,在需要时向人类提供反馈,以推进机器人任务完成。
示例 3:再次考虑示例 1 中的交互场景,机器人任务为示例 2 中的\(\varphi_r = \square \diamond (adj \land major)\)。假设人类为实现自身潜在任务,反复沿对角线放置物体。从机器人视角看,这种人类行为可能使运行轨迹满足\(\varphi_r\),因此机器人应利用这种(非故意的)人类协作来完成任务。
但机器人无法通过 “预先绑定单一策略” 来确保\(\varphi_r\)的满足(无论人类行为如何)。例如,若机器人预先选择 “通过 t1 状态的配置满足\(\varphi_r\)” 的固定策略,而人类仍坚持沿对角线放置物体,双方交互会陷入循环,\(\varphi_r\)永远无法满足。相反,机器人需通过局部观察识别 “人类系统性沿对角线放置物体” 这一行为,并自主选择能导向 t2 状态的动作 ——t2 状态的配置既能容纳人类的对角线放置行为,又能满足\(\varphi_r\)。当然,这一过程的前提是\(\varphi_r\)与人类潜在任务可同时满足。
若双方目标冲突,仅靠机器人适应人类行为不足以解决问题。例如,假设人类持续执行 “h2→r3” 和 “h3→r4” 的动作,此时机器人需识别出 “人类行为已无法用于(非故意的)协作”,并向人类提供反馈 —— 例如,请求人类移除(2,2)格子中的物体(通过执行 “h3→t1” 动作)。
3 基于宽容式策略模板的适应与反馈机制
为分析机器人针对 LTL 任务的策略行为,我们首先将 “规划域 + LTL 任务” 转化为 “人机双人博弈”(这是该领域的常用方法 [43]),随后利用图博弈中最新提出的 “宽容式策略模板”[31][32] 解决上述问题 1。
3.1 ω- 正则博弈
作为第一步,我们引入 “双人(轮流行动)ω- 正则博弈” 的概念,该概念是本文框架的基础。
定义 1:双人(轮流行动)ω- 正则博弈是一个二元组\(G = <D, \Omega>\),其中:
- \(D = <S, s_0, A, AP, L>\):反应型规划域(定义见 2.1 节);
- \(\Omega \subseteq S^\omega\):无限状态序列的 ω- 正则集合,定义了博弈的 “获胜条件”。
这类 ω- 正则博弈可标准地表示为 “parity 博弈”[43]。Parity 博弈是 ω- 正则博弈的一种特殊形式,其获胜条件\(\Omega = Parity[c]\)由 “着色函数”\(c: S \to \mathbb{N}\)定义 —— 该函数为每个状态分配一个自然数(颜色)。若运行轨迹\(\rho\)中 “无限次出现的最大颜色为偶数”,则\(\rho \in Parity[c]\)。通过标准技术 [43],可将 “规划域 + LTL 任务” 转化为 parity 博弈,具体形式化定义如下:
命题 1:给定反应型规划域D和基于AP的 LTL 公式\(\varphi\),可构造 parity 博弈\(G = <D’, \Omega>\),满足以下条件:
- D的运行轨迹与\(D’\)的运行轨迹存在一一对应关系;
- D的运行轨迹\(\rho\)满足\(\varphi\),当且仅当\(D’\)中对应的运行轨迹\(\rho’\)属于\(\Omega\)。
3.2 宽容式策略模板
在双人博弈中,“策略模板” 通过对智能体动作的局部约束,简洁地表示无限多个策略,是对 “策略” 概念的扩展。形式化而言,智能体i的策略模板\(\Pi_i\)包含以下三类约束:
- 不安全动作\(U \subseteq A_i\):智能体禁止执行的动作;
- 共活动作\(Co \subseteq A_i\):在任何运行轨迹中,智能体最多执行有限次的动作;
- 活组\(H \subseteq 2^{A_i}\):动作集合,若某活组\(H \in H\)的源状态被无限次访问,则智能体必须无限次执行该活组中的至少一个动作。
若运行轨迹\(\rho\)满足策略模板\(\Pi_i\)的所有约束,则称\(\rho\)“符合”\(\Pi_i\)。若所有\(\pi_i\)- 轨迹均符合\(\Pi_i\),则称策略\(\pi_i\)“遵循”\(\Pi_i\),记为\(\pi_i \vDash \Pi_i\)。关于策略模板的详细形式化定义及更多解释,可参考 [31]。
最新研究 [33] 表明:在人机 parity 博弈中,可合成一对策略模板\((\Pi_r, \Pi_h)\)(分别对应机器人和人类),其中:
- \(\Pi_h\)捕捉所有能实现协作的人类行为;
- \(\Pi_r\)包含所有 “能对抗协作人类行为、确保获胜条件满足” 的机器人策略。
命题 2:给定 parity 博弈\(G = (D, \Omega)\),可合成机器人与人类的策略模板对\((\Pi_r, \Pi_h)\),满足以下条件:
- 所有属于\(\Omega\)的运行轨迹\(\rho\)均符合\(\Pi_h\);
- 所有遵循\(\Pi_r\)的策略\(\pi_r\)(即\(\pi_r \vDash \Pi_r\))均能确保:所有符合\(\Pi_h\)的\(\pi_r\)- 轨迹均属于\(\Omega\)。
示例 4:针对图 2 中 “机器人任务为\(\varphi_r = \square \diamond (adj \land major)\)” 的网格世界场景,可根据命题 1 构造 parity 博弈 —— 该博弈与图 2 中的规划域结构相同,但需为各状态分配适当的颜色:
- 满足 “\(adj \land major\)” 的状态(即无物体相邻且多数格子被占据)分配颜色 2(偶数);
- 其他状态分配颜色 1(奇数)。
这种着色方式捕捉了机器人的目标 —— 反复到达 “无物体相邻且多数格子被占据” 的状态。通过命题 2 中的合成过程,可计算得到人机策略模板对\((\Pi_r, \Pi_h)\),以捕捉协作行为。例如,人类策略模板\(\Pi_h\)包含活组\(\{h3 \to t1\}\)(图 2 中绿色虚线所示的其他活组也包含在内),这一约束确保人类不会持续阻碍机器人任务推进(如示例 3 中所述)。类似地,机器人策略模板\(\Pi_r\)包含的活组可确保:只要人类遵循\(\Pi_h\),机器人就能始终到达满足 “\(adj \land major\)” 的状态。
3.3 适应与反馈机制
命题 2 的结果为 “捕捉协作行为”(即问题 1 的要求 1)提供了基础,但并未直接解决 “适应” 和 “反馈” 问题(即问题 1 的要求 2 和 3)。为此,本文提出以下框架:利用策略模板\((\Pi_r, \Pi_h)\)的宽容性,让机器人基于\(\Pi_r\)调整策略,并基于\(\Pi_h\)向人类提供反馈。
3.3.1 适应机制
由于\(\Pi_r\)为每个状态提供了一组可选动作,机器人无需预先绑定单一策略。相反,在运行时,机器人会从当前状态的\(\Pi_r\)允许动作集中随机选择动作。这种方式让机器人在再次访问同一状态时,能调整动作选择。具体而言,若机器人某次选择的动作未带来理想结果(如人类表现出不协作行为),运行轨迹最终会回到同一状态,此时机器人可通过随机性从\(\Pi_r\)的允许动作集中选择其他动作。该适应机制可有效满足问题 1 的要求 2。
3.3.2 反馈机制
为实现问题 1 要求 3 中的 “可调反馈机制”,本文引入反馈阈值\(\alpha \in [0,1]\)—— 该阈值决定机器人向人类提供反馈的频率。需注意以下规则:
- 对于\(\Pi_h\)中的 “不安全动作”:这类动作是人类为确保机器人任务完成必须避免的动作,因此只要当前状态存在不安全动作,机器人会立即告知人类;
- 对于\(\Pi_h\)中的 “共活动作” 和 “活组”:机器人会观察人类动作,统计人类违反这些约束的频率(即执行共活动作、或避免执行活组中动作的次数占比)。当违反频率超过\(\alpha\)时,机器人从下一时刻开始提供反馈,直至违反频率低于\(\alpha\)。
根据命题 2,只要人类遵循\(\Pi_h\),机器人策略就能确保任务完成。这种反馈机制让机器人仅在人类行为显著偏离\(\Pi_h\)捕捉的协作行为时,才提供反馈,可有效满足问题 1 的要求 3。
示例 5:延续示例 4 的场景,机器人可在运行时通过 “从\(\Pi_r\)允许动作集中随机选择动作” 调整策略。例如,若人类如示例 3 所述持续沿对角线放置物体:
- 假设机器人当前处于状态 h0,且原本计划通过 t1 状态的配置推进任务;
- 若人类继续沿对角线放置物体(即执行 “h0→r1” 动作,该动作违反\(\Pi_h\)中的活组\(\{h0→r0\}\)),机器人会调整策略,选择导向 t2 状态的动作 ——t2 状态的配置既能容纳人类的对角线放置行为,又能满足\(\varphi_r\)。
再考虑另一种场景:若人类为实现自身潜在任务,持续执行 “h2→r3” 和 “h3→r4” 动作(如示例 3 所述,该行为会阻碍机器人任务)。当人类违反活组约束的频率超过反馈阈值\(\alpha\)时,机器人会向人类提供反馈,请求其执行活组动作 “h3→t1”—— 该动作能帮助机器人推进\(\varphi_r\)的完成。
4 实验
我们在两个实验场景中评估了所提框架,以体现该新颖 HRωI 框架的不同优势:
- 积木操作场景:在物理机器人平台上验证方法,场景如图 1 所示(对应示例 1-5)。该场景为 “观察机器人如何基于人类动作在线调整策略、并在人类阻碍任务超过阈值时提供可调反馈” 提供了可解释的测试平台;
- Overcooked-AI 环境:这是协作规划的标准基准测试平台 [40],可体现 “指导与适应能力” 在 “自主涌现复杂人机策略性交互” 中的作用。尤其值得注意的是,ω- 正则规范的天然结构让我们能研究 “人机任务从完全一致到部分 / 完全冲突” 等不同难度下的新兴交互。
这两个实验共同表明:该方法在符号域中具备透明度,且能在运行时自主生成远超现有方法能力的复杂人机策略性交互。
注 1:Schuppe 等人 [22] 也研究了 “机器人向人类提供建议” 的人机交互场景(“Follow My Advice”,FMA),但其方法聚焦于 “为人类计算充分假设”,并基于预计算的机器人策略设计静态反馈机制,以实现有限时间范围的目标。与之不同,本文框架强调 “机器人策略基于人类行为的在线适应”,并采用可调反馈机制处理持续的 ω- 正则目标 —— 这一点已在下文实验中得到验证。若要将两种方法直接对比,需将本文场景重构为有限时间范围任务,但这会削弱本文框架 “聚焦适应与反馈协同以实现持续目标” 的核心价值。
4.1 网格世界积木操作
在该实验中,我们在 Franka Emika Panda 机械臂(运行 ROS Jazzy 系统)上实现了简化的网格世界积木操作场景,以验证框架在抽象模型之外的可行性。实验设置如下:机械臂在 3×3 工作空间内操作实体积木(可放置或移除),与示例 1 中描述的状态完全对应。人类通过放置红色积木与工作空间交互,机器人则放置蓝色积木。系统会实时监测积木配置,并评估机器人任务规范(如 “保持积木不相邻”)是否当前满足。
该演示背后的反应型规划域包含约 7000 个状态和 18 个命题,编码了 “人机物体的所有可能放置方式” 及 “合法的轮流动作”。我们的实现需约 6 秒完成 parity 博弈的构造和策略模板的合成(该过程在执行前离线完成)。在执行阶段,机器人遵循自适应策略:
- 基于观察到的人类动作更新自身动作;
- 当人类行为可能阻碍任务完成时(如示例 3 所述),通过显示屏生成反馈。
图 1 展示了该实验设置的实物图,体现了抽象域在真实世界中的实现方式。该实验表明,我们的框架能从形式化模型扩展到真实场景,为评估 “适应能力” 和 “人类反馈” 提供了可解释的测试平台。
4.2 Overcooked-AI
我们在 Overcooked-AI 环境 [40](多智能体协作规划的常用基准测试平台)中进一步评估了框架。在该环境中,人机需反复执行烹饪任务,目标是持续制作汤品。双方各有独立的 LTL 任务(编码为食谱规范),且任务彼此保密。
4.2.1 实验场景设计
我们设计了三类实验场景,以 “人机食谱的关系” 为区分标准:
- 完全一致:人机食谱相同,双方在不知情的情况下执行同一任务;
- 兼容:人机食谱不同,但存在至少一种汤品能同时满足双方规范;
- 冲突:人机食谱不同,且不存在任何能同时满足双方规范的汤品。
这三类场景涵盖了 “人机任务从完全一致到完全冲突” 的不同错位程度。表 1 总结了实验中使用的食谱配置。
表 1 Overcooked-AI 实验中的食谱配置
| 场景 | 机器人食谱 | 人类食谱 |
|---|---|---|
| 完全一致 | 需 3 个洋葱 | 需 3 个洋葱 |
| 冲突 | 需 3 个洋葱 | 需 2 个洋葱 |
| 兼容 | 需 2 个洋葱(切半) | 需 2 个洋葱(整个) |
4.2.2 环境建模与实验流程
Overcooked-AI 环境天然适合 “持续任务” 的实现 —— 人机需反复完成食谱。每个食谱规范对应一个 ω- 正则目标:若运行轨迹中 “符合要求的食谱被无限次执行”,则该轨迹满足任务。这一特性让我们不仅能评估 “单一目标是否达成”,还能评估 “人机任务是否能持续满足”。
我们按照 2.1 节的定义,将 Overcooked-AI 环境建模为反应型规划域:
- 状态:编码 “人机位置”“食材位置”“汤品烹饪状态”;
- 动作:对应双方可执行的 “移动” 和 “交互指令”;
- ω- 正则任务:通过 “状态上的 parity 条件” 定义(可从食谱规范推导得出)。
该域包含约 68000 个状态和 200 多个命题(编码环境相关特征)。我们通过命题 2 中的合成过程,计算得到人机策略模板对\((\Pi_r, \Pi_h)\)(捕捉协作行为)—— 该过程需约 3 分钟(执行前离线完成)。执行阶段,机器人按照 3.3 节描述的 “适应与反馈机制” 运行,人类行为则通过 “符合其食谱的概率策略” 模拟。
4.2.3 实验参数与指标
我们在三类场景中,分别采用不同的反馈阈值\(\alpha\)(范围为 0.00-0.10)进行实验。每个场景的实验流程如下:
- 运行系统直至交付 10 份汤品;
- 每次运行最多 500 步动作,执行时间约 1 分钟;
- 为消除 “人机动作选择随机性” 的影响,每个场景重复运行 10 次。
每次运行中,我们记录以下指标:
- 符合机器人食谱的汤品占比;
- 符合人类食谱的汤品占比;
- 同时符合双方食谱的汤品占比;
- 机器人提供反馈的频率。
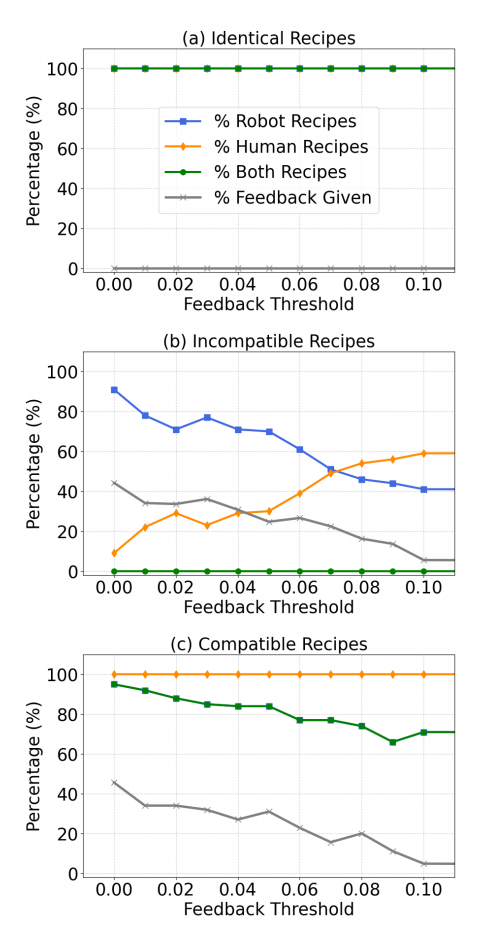
图 3 展示了所有场景中这些指标的时间演化过程,体现了 “适应能力” 和 “反馈” 对 “持续任务满足” 的影响。
4.2.4 实验结果分析
(1)完全一致场景
在该场景中,人机在不知情的情况下执行相同食谱规范。如图 3(a)所示,所有运行中,人机食谱均能持续满足,且机器人从未提供反馈。这一结果体现了 “适应能力” 的优势:即便人机初始采用不同策略执行同一食谱,机器人也能通过在线调整,使双方行为自然对齐。若系统缺乏适应能力,可能需要通过反馈协调双方策略;而我们的框架能让协作在运行时自主涌现。值得注意的是,这一结果也凸显了本文框架相比 [22] 中 “静态反馈机制” 的优势(见注 1)——[22] 的方法即便在人机任务完全一致时,也会因 “无法在线调整机器人策略” 而提供不必要的反馈。
(2)冲突场景
在该场景中,人机食谱规范完全冲突,不存在同时满足双方的汤品。因此,如图 3(b)所示,“同时符合双方食谱的汤品占比” 始终为 0。但由于任务目标被定义为 ω- 正则属性,只需 “双方食谱最终均能被无限次执行” 即可满足要求。因此,人机可通过 “轮流制作符合各自食谱的汤品” 实现协作。图 3(b)表明,这种直观的协作行为确实能自主涌现,且受反馈阈值\(\alpha\)影响:
- 当\(\alpha\)增大时,机器人对 “人类不协作行为” 的容忍度提高,导致 “符合人类食谱的汤品占比” 上升,“符合机器人食谱的汤品占比” 下降;
- 当\(\alpha = 0.07\)时(阈值选择恰当),人机均能持续满足自身食谱,占比均约为 50%。
这一结果体现了 “反馈阈值调整” 的重要性 —— 通过校准反馈灵敏度,可提升新兴协作行为的质量。
(3)兼容场景
在该场景中,人机食谱不同,但存在同时满足双方的汤品。如图 3(c)所示,所有运行中人类均能持续满足自身食谱,而机器人通过 “策略调整” 和 “反馈” 确保自身食谱也能满足:
- 即便\(\alpha\)较大(反馈较少),机器人通过在线适应策略,仍能在超过 70% 的运行中满足自身食谱;
- 当\(\alpha\)较小时(反馈更频繁),机器人能进一步提升 “双方共同满足” 的比例,最高可达 95%。
这一结果体现了 “适应能力” 与 “反馈调整” 的协同效应 —— 二者结合可实现 “双方食谱的持续满足”。
